Geometri Günlüğü
Tuesday, March 25, 2025
Sunday, March 16, 2025
Wednesday, March 12, 2025
Monday, March 10, 2025
Friday, March 7, 2025
Monday, February 24, 2025
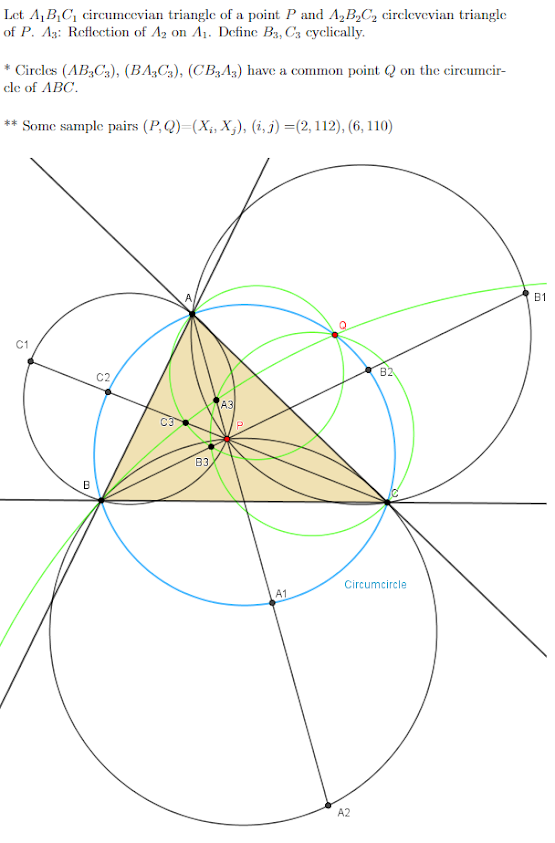
Saturday, November 30, 2024
1988. Circumcenters On Euler Line
Let ABC be a triangle with P, Q are two points on Euler line of ABC.
A',B',C' are inverse images of A,B,C through circle diameter PQ.
* Circumcenter of A'B'C' lies on Euler line of ABC.
Saturday, September 14, 2024
1987. Circumcenter On Euler Line
Let H=X(4)-Orthocenter of ABC. A1B1C1 cevian triangle of H. B1A, C1A are reflections of B1, C1 on A.
LA, line through B1A, C1A. define LB, LC cyclically.
A2B2C2 triangle bounded by lines LA, LB, LC.
* Circumcenter of A2B2C2 lies on Euler line of ABC.
Tuesday, September 3, 2024
Thursday, August 8, 2024
Wednesday, August 7, 2024
Wednesday, July 31, 2024
Sunday, July 28, 2024
Wednesday, July 17, 2024
Tuesday, July 16, 2024
Tuesday, May 28, 2024
Thursday, May 16, 2024
Friday, March 1, 2024
Sunday, February 18, 2024
Tuesday, February 6, 2024
Sunday, February 4, 2024
Friday, February 2, 2024
Thursday, February 1, 2024
1969.Conics Intersecting Cubic Curves At a Fixed Point
Let P be a triangle center on K001-Neuberg Cubic of ABC.
Any line through P intersect the K001-Neuberg Cubic at P1 and P2.*As P1, P2 varies on K001-Neuberg Cubic, the conic {A,B,C,P1,P2} intersect the K001-Neuberg Cubic at a fixed point.
**If P=X(1)-Incenter of ABC, fixed point is X(7164).
If P=X(3)-Circumcenter of ABC, fixed point is X(1138).
If P=X(4)-Orthocenter of ABC, fixed point is X(8431).
If P=X(13)-1st Fermat-Toricelli point of ABC, fixed point is X(8445).
If P=X(399) of ABC, fixed point is X(4).
Monday, January 29, 2024
Sunday, January 28, 2024
Thursday, January 25, 2024
1964. A Construction For X(18569)
Let A1B1C1 reflection triangle of X(3)-circumcenter on the side lines of ABC.
Tangents to circumcircle of A1B1C1 at A1, B1, C1 form a triangle A2B2C2.**Circumcenter of A2B2C2 lies on Euler line of ABC. It's X(18569).
1963. A Triangle Inscribed In Nine-Point Circle
Let A1B1C1 median triangle of ABC.
A2: Inverse of X(3)-Circumcenter of ABC in the circle with diameter B1C1.Define B2, C2 cyclically.
*A2B2C2 is inscribed in the Nine-Point Circle of ABC.
Monday, January 22, 2024
Saturday, January 20, 2024
Wednesday, January 17, 2024
Saturday, January 13, 2024
Sunday, January 7, 2024
Thursday, August 10, 2023
Sunday, July 16, 2023
1955. A Construction For the Perspector Of 2nd Lemoine Circle
Let K=X(6)-Symmedian point of ABC. Antiparallel from K to BC intersect the AB, AC at Ac, Ab resp.
Define Ba, Bc, Ca, Cb cyclically.
KA: Antipode of K respect to circle (KBaCa). Define KB, KC cyclically.
* ABC and KAKB,KC are perspective triangles. Perspector is X(3527) = ISOGONAL CONJUGATE OF X(631)=perspector of 2nd Lemoine circle
Wednesday, May 10, 2023
Saturday, May 6, 2023
Thursday, May 4, 2023
Wednesday, May 3, 2023
Monday, May 1, 2023
Sunday, April 30, 2023
Wednesday, April 26, 2023
Subscribe to:
Comments (Atom)
-
Dedicated to Francisco Javier García Capitán on the occasion of his birthday.



.PNG)









































.PNG)