Monday, January 29, 2024
Sunday, January 28, 2024
Thursday, January 25, 2024
1964. A Construction For X(18569)
Let A1B1C1 reflection triangle of X(3)-circumcenter on the side lines of ABC.
Tangents to circumcircle of A1B1C1 at A1, B1, C1 form a triangle A2B2C2.**Circumcenter of A2B2C2 lies on Euler line of ABC. It's X(18569).
1963. A Triangle Inscribed In Nine-Point Circle
Let A1B1C1 median triangle of ABC.
A2: Inverse of X(3)-Circumcenter of ABC in the circle with diameter B1C1.Define B2, C2 cyclically.
*A2B2C2 is inscribed in the Nine-Point Circle of ABC.
Monday, January 22, 2024
Saturday, January 20, 2024
Wednesday, January 17, 2024
Saturday, January 13, 2024
Subscribe to:
Comments (Atom)
-
Dedicated to Francisco Javier García Capitán on the occasion of his birthday.









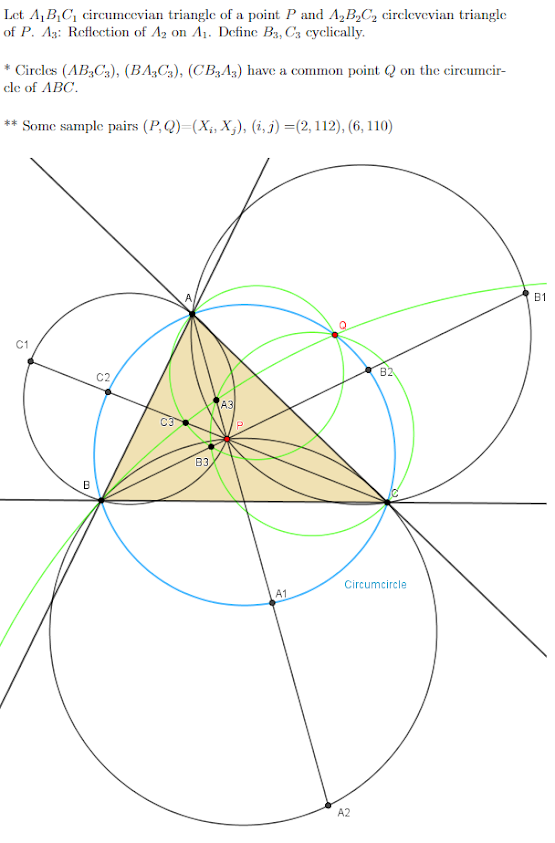



.PNG)