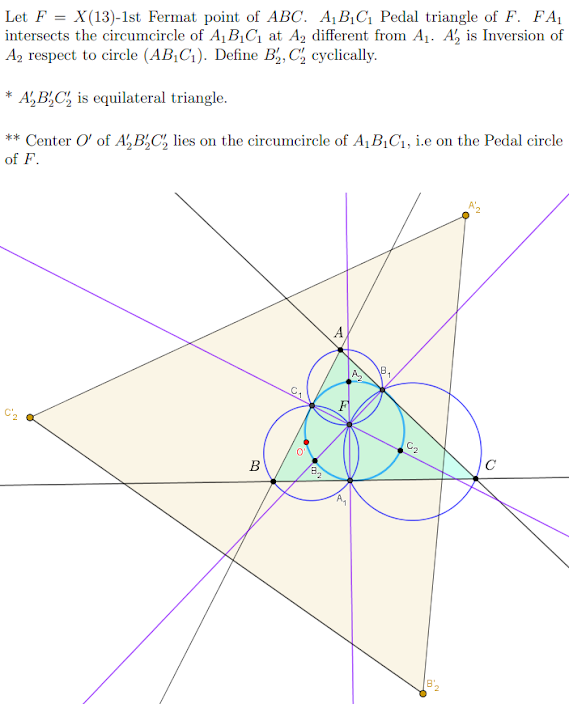
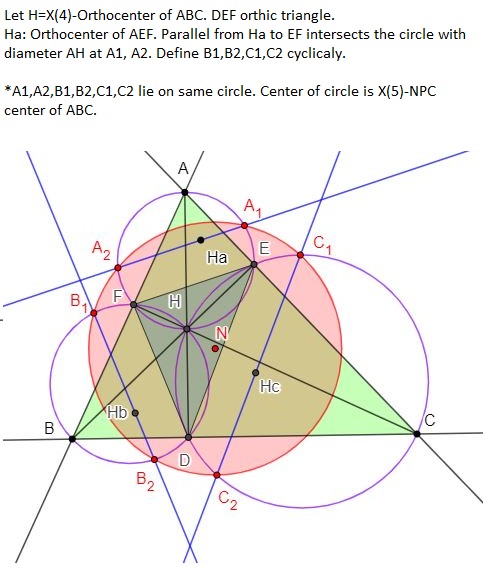
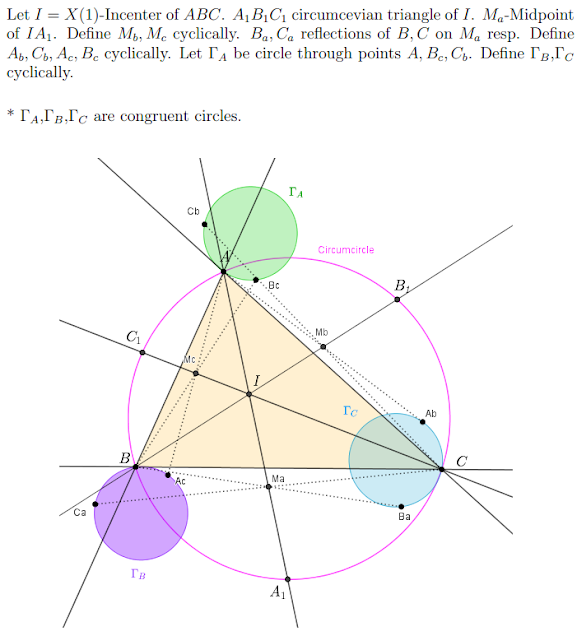
Saturday, April 30, 2022
Friday, April 29, 2022
Thursday, April 28, 2022
Wednesday, April 27, 2022
1832. Inverted Triangles and Circumcenters On Euler Line
Let ABC be a triangle and A1B1C1 is perspective with ABC at a point P and homothetic to ABC.
A2 is inversion of A1 respect to circumcircle of ABC. Define B2, C2 cyclically.
* Circumcenter of A2B2C2 lies on the line OP.
Application. Let P be a point on Euler line of ABC. A1,B1,C2 midpoints of AP, BP, CP resp.
A2 is inversion of A1 respect to circumcircle of ABC. Define B2, C2 cyclically.
** O',Circumcenter of A2B2C2 lies on the Euler Line of ABC.
For P=X(2), O'=X(33532)
For P=X(5), O'=X(?)
For P=X(20), O'=X(12084)
Monday, April 25, 2022
1831. ConConic Triangles
Let P be a point and A1B1C1 cevian triangle of P.
ta= tangent to circumcircle of A1B1C1 at A1. Define tb, tc cyclically.Let A2B2C2 triangle bounded by lines ta, tb, tc.
*A,B,C, A2,B2,C2 lie on same conic.
** For P=X(2), Center of the conic is X(15449)-CENTER OF THE X(2)-ALTINTAS HYPERBOLA.
*** Which is the center of the conic for some triangle centers?
Thursday, April 14, 2022
Tuesday, April 12, 2022
1829. Constructions For X(14790) and X(18569)
1. Let O=X(3) circumcenter of ABC. Ha, Hb, Hc orthocenters of OBC, OCA, OAB resp.
La=Antiparallel from Ha to BC. Define Lb, Lc cyclically.Let A1B1C1 triangle bounded by lines La,Lb,Lc.
* Orthocenter of A1B1C1 lies on Euler line of ABC. Its X(14790)= Conjugate-Couple of X(22) In the Range In Involution {X(2),X(5)}, {X(3),X(4)}.
2.Let H=X(4) orthocenter of ABC. Oa, Ob, Oc circumcenters of HBC, HCA, HAB resp.
La=Antiparallel from Oa to BC. Define Lb, Lc cyclically.
Let A1B1C1 triangle bounded by lines La,Lb,Lc.
* Circumcenter of A1B1C1 lies on Euler line of ABC. Its X(18569)= Ehrmann-Side-Ehrmann-Vertex Similarity Image of X(382).
Sunday, April 10, 2022
Tuesday, April 5, 2022
Monday, April 4, 2022
Sunday, April 3, 2022
Friday, April 1, 2022
Subscribe to:
Comments (Atom)
-
Dedicated to Francisco Javier García Capitán on the occasion of his birthday.












.PNG)